金刚石锯片模态实验中传递函数的确定:
对于N自由度的振动系统,假设该阻尼成比例性,在这种简化情况下,多数是符合实际要求的,对式(2-1)两边进行拉普拉斯变换,且假定{x(O)}=0和{x(O)}=0,可得

式(2-4)中的adt(s)称作振动系统的特征方程,是Z(s)的行列式。传递函数矩阵可通过线性代数计算的方法改写为

若s=jω,应用拉普拉斯变换转化为傅里叶变换,通过传递函数矩阵变换成频响函数矩阵,基于定理得到振动系统在频域内输出和输入的关系可表示为
χ(ω) = H(ω)F(ω) (2-10)
基于振型矩阵的加权正交条件,假定振型矩阵C可由阻尼矩阵[Φr]对角化则动态矩阵可表示为

基于模态参数表示的频率响应函数:

公式(2-14)可以概述为j点单独激振时,i点测得响应函数Χi(t)与激振力fj(t)的傅里叶比值。由于一般来说Z(S)是对称矩阵,所以H(ω)称为矩阵,因此可以得出以下关系式:
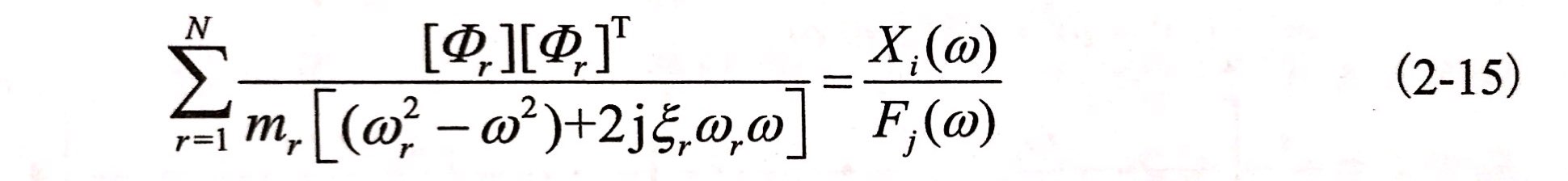
频响函数的互易性是检验频响测试精度的一项重要指标,由此说明测得频响函数某一矩阵的一行或是一列就可确定结构的全部模态函数。
这就是金刚石锯片模态实验传递函数的确定方法。
