参考资料可得,最小二乘法和神经网络法是比较常用的方法,但是,对于钎焊金刚石锯片的检测数据来说,神经网络法比最小二乘法更具有非线性,因此,对BP神经网络原理进行分析。
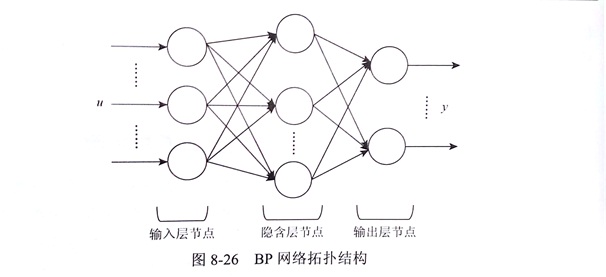
BP网络是一种单向传播的多层前向网络,由输入层 (inputlayer)、隐含层 (hide layer) 和输出层 (output layer) 节点构成,每一层节点的输出只影响下一层节点的输出,其网络结构如图 8-26 所示。其中u和y分别为网络输入、输出向量,每个节点表一个神经元。
可将u 端放入采集的缺陷电压信号,在y端放入缺陷长度和深度。钎焊切割片检测系统数的BP神经网络结构的隐层节点可为一层或多层,同层节点没有任何耦合,前层节点到层节点通过权连接。输入信号从输入层节点依次传过各隐层节点到达输出层节点。
BP网络具有以下两个特点:
(l)信息的前向传播处理。从信息处理的处理理解,网络中的节点一般分为两类:一类是网络输入端节点,它负责将外界信息输入神经网络中;另一类是隐含层或输入层节点, 它可以对输入节点内的信息进行处理。
从图可看出,在息的处理过程中,信息从输入层输入, 上一层的输出是下一层的输入,信息逐层传递 ,没有反馈回路。
(2) 误差的后向传播修整,即误差反传算法。误差由输出层逐层反向传至输入层,有误差修改网络权值,直至得到网络权值适应学习样本。其最终目的是使网络中每一输出单元的实际输出在某种意义上逼近应有输出。
一旦选定了目标函数形式,误差纠正学习规则就变成了一个典型的最优化问题。误差反传算法可简化为以下步骤:
① 网络初始化,随机设定权值和阈值的初始值;
② 具有上述初始值的神经网络提供输入学习样本和序号;
③ 计算隐层单元输出值;
④ 计算输出层单元的输出;
⑤ 计算输出层单元偏差;
⑥ 判断均方误差是否满足给定允许偏差,当满足时转到⑧,否则继续执行后再由③顺序进行;
⑦ 修正权值;
⑧ 结束训练。
以上就是对钎焊金刚石锯片检测的神经网络法的分析。
